Covariance
In general, Covariance is a statistic measure of joint variability between two variables. You can learn more statistical docs on the web, but this article focuses on the business usage in Datama Compare.
In our case, covariance is basically the share of the variation that you can’t attribute to one of the effect you’re trying to split out.
In waterfall analysis, the different effects are the different steps that you’ve defined within Metric Relation.
A basic example
You want to analyze your Revenue (A) variations between Last Year ( Start ) and with This Year (End)
For business reasons, you may want to split your Revenue (A) between Volume (B) and Price (B/A) .
So what you want, is to really explain Revenue_ThisYear – Revenue_LastYear. (A_End - A_Start)
Well, this can be written as following:
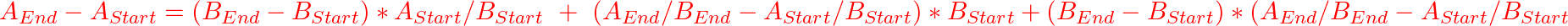
The visual representation below is much easier to get:
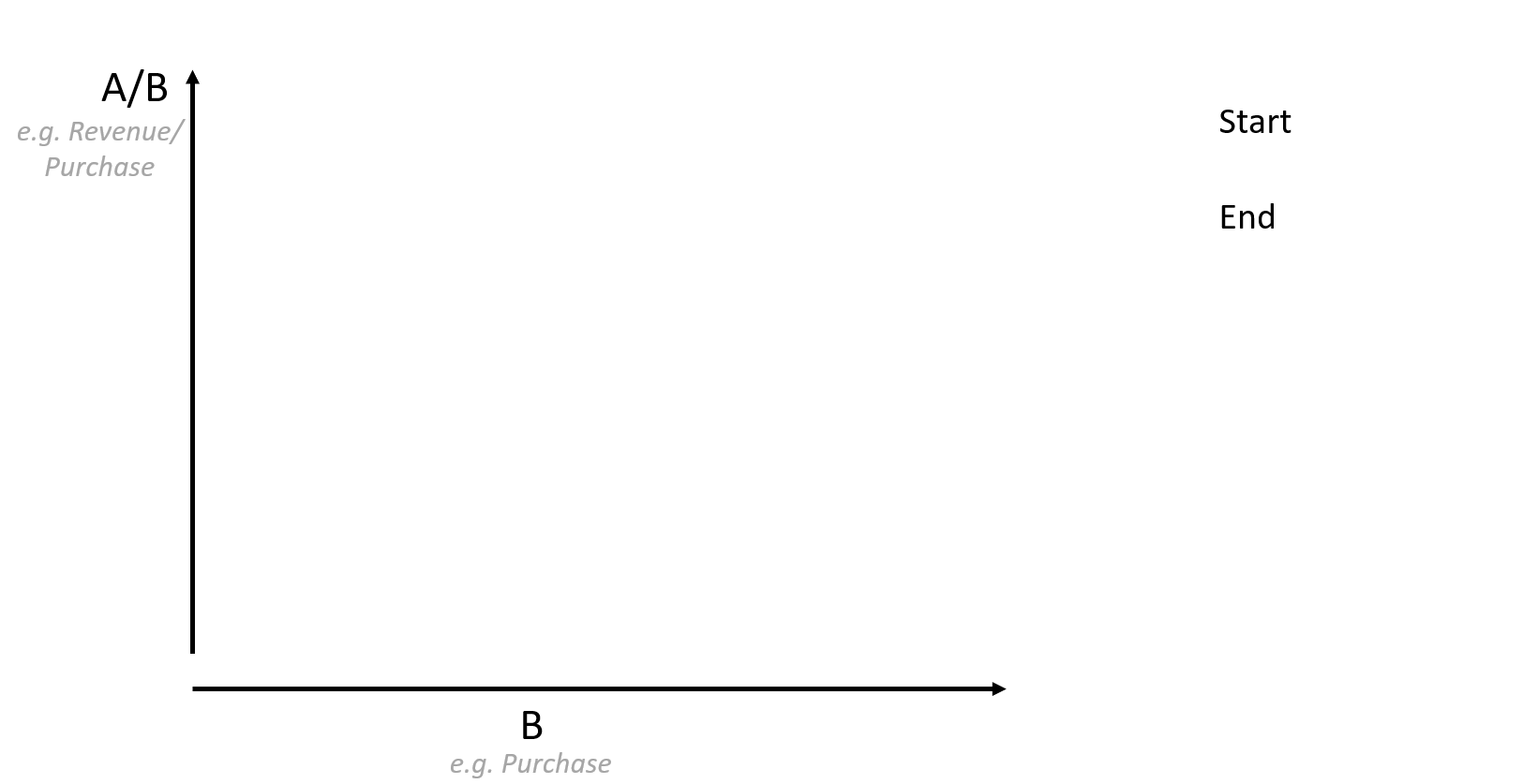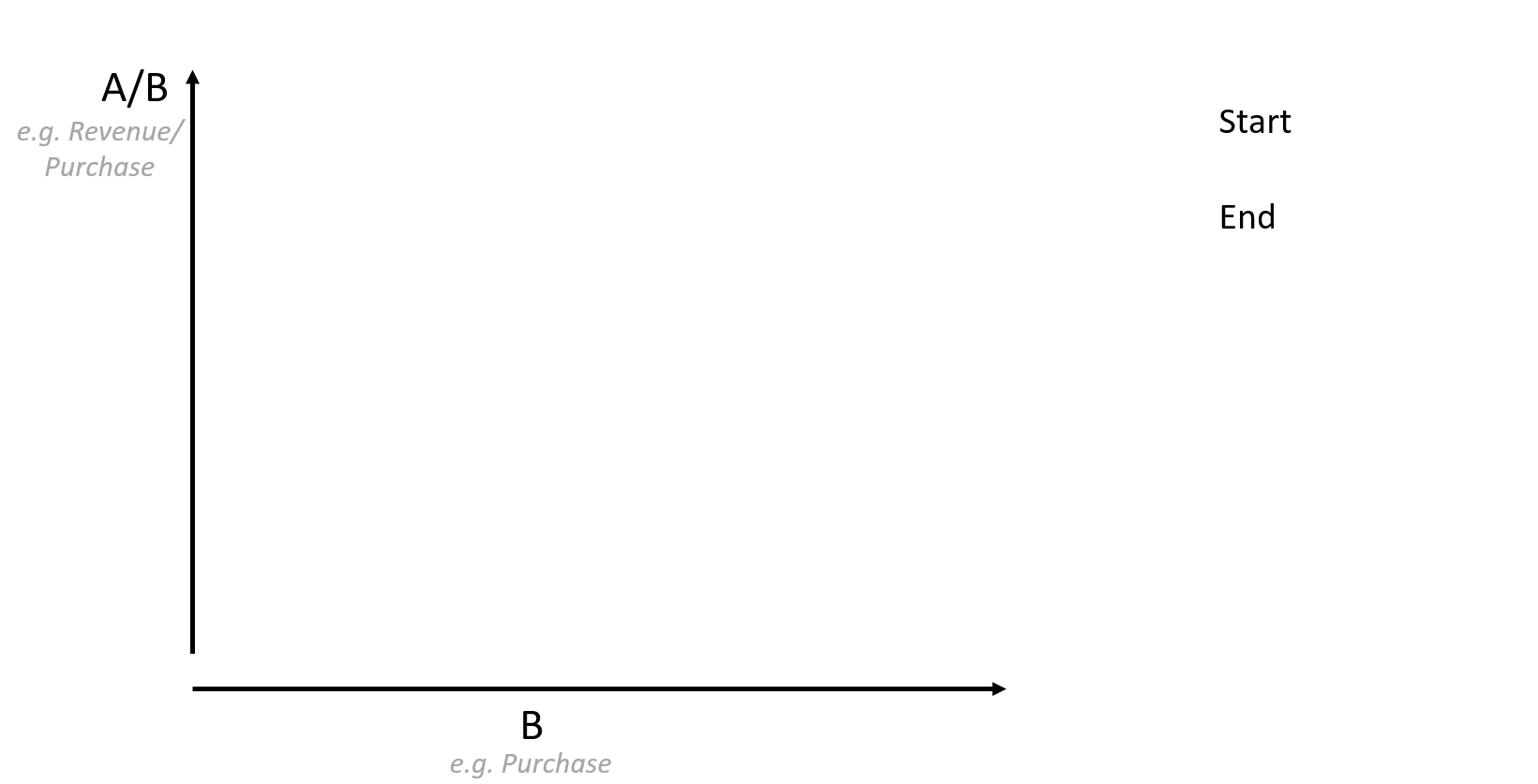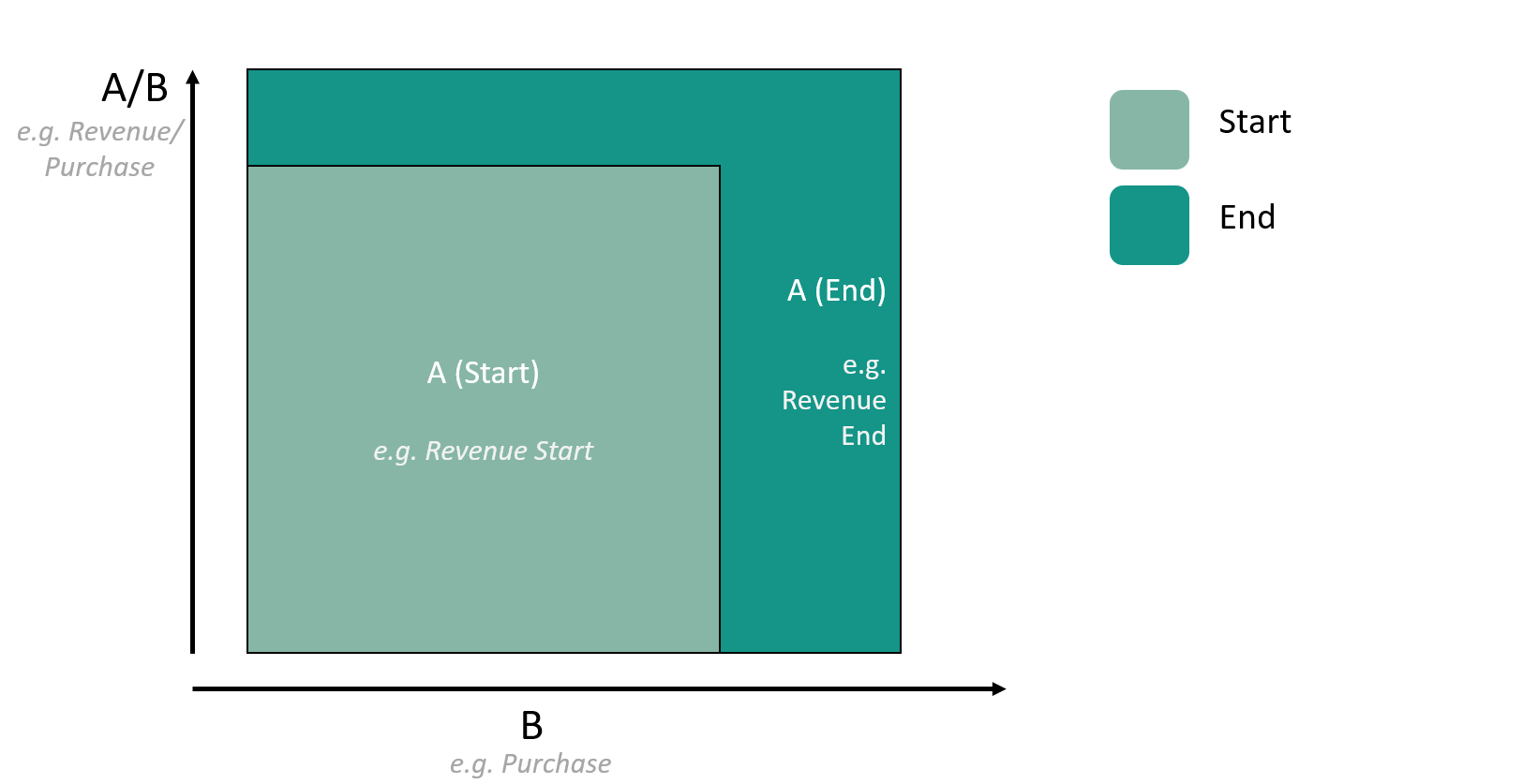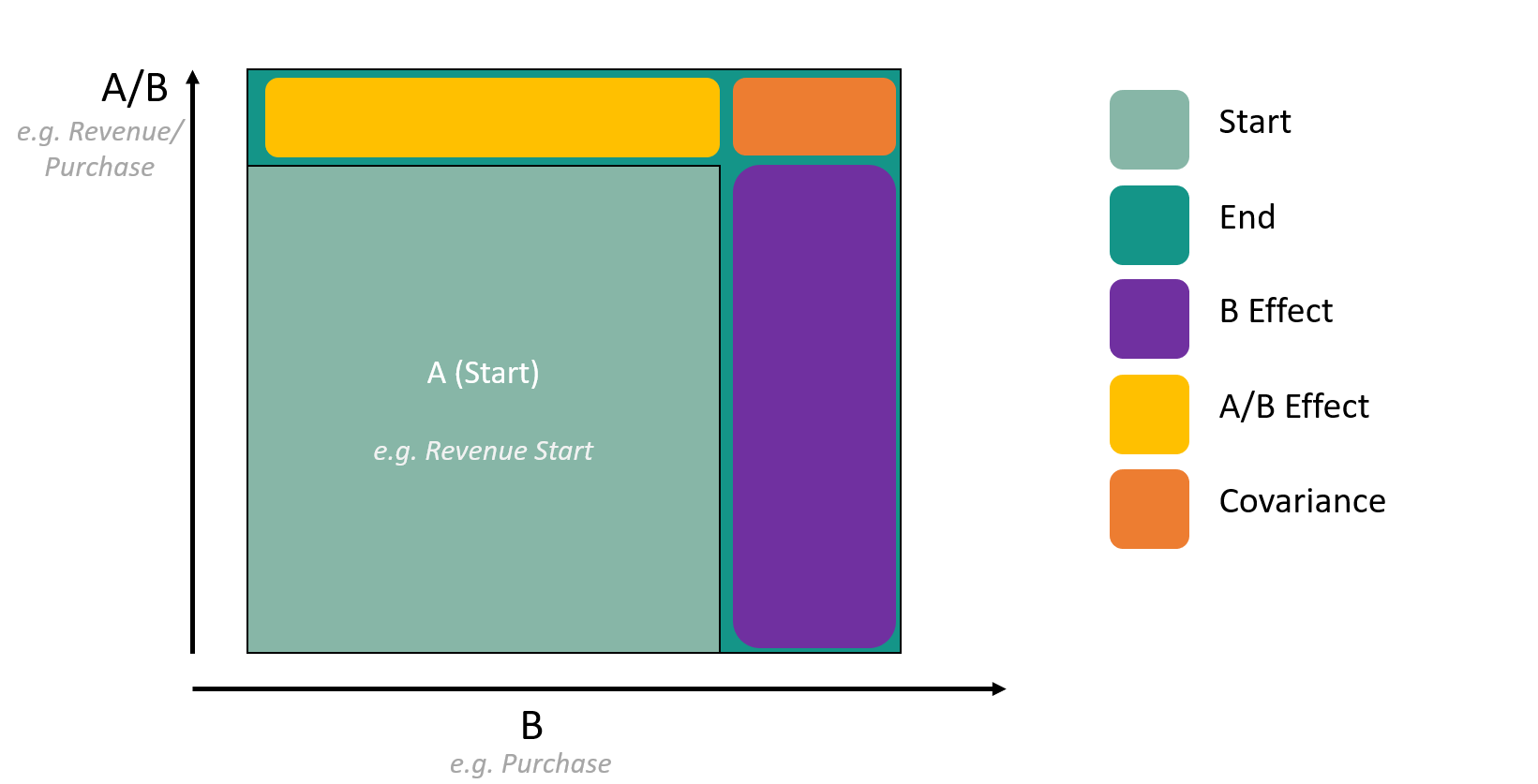
What you want to explain is the gap in surface between the two green squares.
Well, you just split it into B effect (Purple), A/B effect (Yellow) and Covariance (Orange).
How it impacts Waterfall analysis
The above maths is great, but hard to show and explain to a business man that just want to understand why its revenue went down, or up.
So, in order to display this in a waterfall, with just volume and price effect -or whatever steps you’ve defined-, we just re attribute the covariance to each other effect, proportionally to its size.
The % of Covariance that we display in Datama Compare charts is the ratio between the Covariance and the overall gap you’re trying to explain.
We put a flag (!) when Covariance gets high (>30%), but the analysis remains true. Just think that the effects you’re trying to sort out are not fully independent, so sometimes it’s not one effect (e.g. Price) or the other (e.g. Volume) that affects your overall KPI (e.g. Revenue), but both at the same time. And that’s your Covariance!